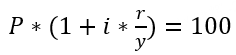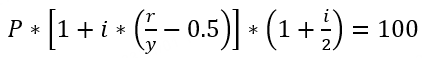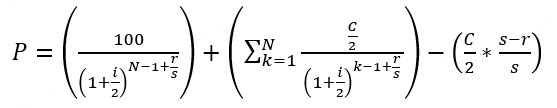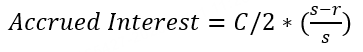国债信息 | 解释 |
债券价格 | 债券价格是买入这张债券的价格,这个数据在交易时间内可能随时变动。 |
票面息率 | 票面息率(Coupon Rate)是指债券发行时上面标明的、用于计算债券每年支付给持有人的固定利息金额的百分比。它是债券面值(或称为票面价值)上所载的固定年利息数额与面值的比率。 例如,如果一张债券的面值为1,000美元,票面息率为5%,那么每年该债券将支付给持有人50美元的利息(1,000美元× 5%=50美元)。票面息率通常在债券发行时确定,它决定了投资者可以在持有期间获得的固定利息收入。 |
到期年化收益率 Yield to Maturity,YTM | 债券的到期年化收益率(Yield to Maturity,YTM)是指如果持有该债券直至到期,并且在此期间收到了所有的利息和本金支付,那么投资者将在债券投资上获得的年化收益率。YTM考虑了投资者购买债券时的价格、债券的票面价值(即债券的面值,到期时投资者将获得的本金)、债券的到期期限、以及债券上的利息支付频率等因素(未考虑交易佣金成本)。 按到期收益率对债券所有未来的现金流进行折现,所得到的现值应和买入价格相等,即未来得到的利息支付和最终本金偿还的现值总和,应等于债券当前的市场价格。 对于不同的债券品种,YTM的计算公式有所不同:
【以上公式的相关参数】
|
派息频率 | 派息频率是指这张国债一般会按照怎样的时间频率进行派息,美国国债notes和bonds目前基本都是一年约定两次派息。 |
剩余年限 | 剩余期限是从现在买入至该国债到期,还剩余多少年限。 |
到期日 | 是指国债的到期日期。 |
交易执行日 Execution date | 交易达成的日期,但还未发生债券所有权的转移。 |
交易结算日 Settlement date | 交易最终完成的日期,买方必须向卖方付款,同时卖方将资产交付给买方。为执行日后一天。应计利息的计算以结算日为准。 |
买卖盘口 | 买盘上显示了投资者愿意支付的最高价格和该价格对应的到期年化收益率。卖盘上显示了投资者愿意接受的最低价格和该价格对应的到期年化收益率。 债券买卖盘口报价通常只能作为参考,而不是确定性的交易价格。 |
买入参考价 Bid Price | 买入参考价(Bid Price),指从平台处买入债券的参考价格,T-Bill的报价通常为利率,即Discount Rate;Bond和Note的报价通常为价格。报价不含交易佣金和应计利息。 |
卖出参考价 Ask Price | 卖出参考价(Ask Price),指把自己持有的债券卖出时,买方支付的参考价格。 |
中间价 | 是指市场上的买入价格和卖出价格之间的中间点。投资者可使用中间价作为参考,因为它通常反映了市场上的供需情况。 |
久期 | 久期(Duration)是一个用于衡量债券价格对利率变化的敏感度指标,它可以帮助你预测债券价格在市场利率上升或下降时的变化方向和幅度。 |
麦考利久期 | 麦考利久期(Macaulay Duration) 是债券的一个关键金融指标,它表示投资者持有一份特定债券后,收回其投资的平均期限。麦考利久期是对债券的现金流支付时间进行加权平均的结果,包括了债券的本金和利息支付。该指标的数值代表了债券的平均期限,以年为单位。 麦考利久期的意义在于,它帮助投资者了解债券的平均剩余期限,以及在此期限内所能获得的现金流。这个指标也用来衡量债券价格对利率变动的敏感度。当麦考利久期较长时,表示债券的现金流主要集中在较远的将来,因此债券的价格更容易受到市场利率波动的影响。 麦考利久期的数值越高,说明债券的本金回收期较长,价格波动幅度相对较大;反之,麦考利久期较短的债券,在市场利率变动时,其价格波动较小。 |
修正久期 | 修正久期(Modified Duration)是用来衡量债券价格对利率变动的敏感度的指标。它衡量了债券价格在市场利率变动时的相对变化幅度。修正久期的计算基于麦考利久期(Macaulay Duration) 并乘以债券的收益率(或者利率变动的百分比变化)。它通常用来估计债券价格在利率变动时的变化幅度。 在实际应用中,修正久期可用于估算债券价格的变化。例如,如果一个债券的修正久期为5年,那么当市场利率上升1%时,该债券的价格大约会下降5%。 |
凸性 | 债券的凸性(Convexity)是指债券价格对于利率变化的曲线度量。 它是一个用来衡量债券价格变动相对于利率变动的二阶导数。凸性提供了比修正久期(Modified Duration)更精确的信息,因为它考虑了债券价格与利率的非线性关系。 在金融领域,债券价格与市场利率之间的关系通常是非线性的。当利率上升或下降时,债券价格的变化速度并不是线性的,而是呈现出曲线状。凸性度量了这种非线性关系。 凸性通常用于修正久期的估计,因为它提供了更准确的价格变动信息。修正久期只考虑了价格和利率之间的线性关系,而凸性则可以提供关于价格和利率之间曲线关系的更详细信息。在债券组合管理和风险管理中,了解债券的凸性非常重要,因为它有助于更精确地估计债券组合在不同市场利率下的价格变化。 |
应计利息 | 债券的应计利息(Accrued Interest)指的是在债券的最后一个付息日(或称到期日)之后,但在债券出售日期之前所累积的未付利息。 当投资者在一个付息周期的中间时间购买债券时,他们必须支付截至购买日期的应计利息给卖方。在债券的下一个付息日期,投资者能收到全额的利息。应计利息通常是基于债券的票面利率和购买日期之间的实际天数进行计算的。 应计利息不是费用,而是买家支付给卖家的持有期间的利息,虽然债券一般是半年才派息一次,但是买入持有之后每天都会计算应计利息,交易时买家需要支付这部分钱给卖家。应计利息会在派息之后清空并重新计算。 其中,C=票息,s = 当前付息期总天数,r = 当前付息期剩余天数 举个例子来说明应计利息:2021/12/18发行的5年期note,票息 = 5,到期日为2026/12/18。当前结算日为2023/10/31,下一付息日期为2023/12/18,上一付息日期为2023/06/18. 故:s = 下一付息日 - 上一付息日 = 2023/12/18 - 2023/06/18 = 183天 r = 下一付息日 - 结算日 = 2023/12/18 - 2023/10/31 = 48天 Accrued Interest = 5/2 * (183 - 48) / 183 = 1.84426 暂时无法在飞书文档外展示此内容 注:执行日(Execution Date)是交易达成的日期,但还未发生债券所有权的转移; 结算日(Settlement Date)是交易最终完成的日期,买方必须向卖方付款,同时卖方将资产交付给买方。为执行日后一天。 应计利息的计算以结算日为准。 具体的天数根据当期实际天数计算。Bonds and notes issued by the U.S. Treasury earn interest calculated on an actual/actual basis. 所以,如果你在 10 月 31 日购买了这张国债,你需要支付给卖家大约 1.84 美元的应计利息,以补偿他应该获得的利息。然后,在当年的 12 月 18 日,你将获得全部利息支付。 (注意:以上案例为方便理解,采用应计利息的通用算法,每个机构对于“计息系数”定义不同,需要以实际计算结果为准) |