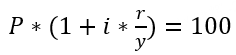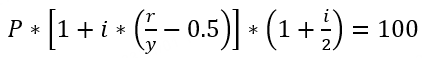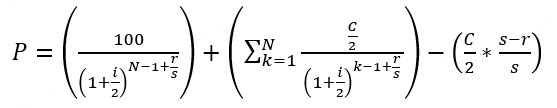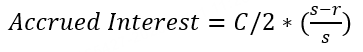國債信息 | 解釋 |
債券價格 | 債券價格是買入這張債券的價格,這個數據在交易時間內可能隨時變動。 |
票麵息率 | 票麵息率(Coupon Rate)是指債券發行時上麵標明的、用於計算債券每年支付給持有人的固定利息金額的百分比。它是債券麵值(或稱為票麵價值)上所載的固定年利息數額與麵值的比率。 例如,如果一張債券的麵值為1,000美元,票麵息率為5%,那麼每年該債券將支付給持有人50美元的利息(1,000美元× 5%=50美元)。票麵息率通常在債券發行時確定,它決定了投資者可以在持有期間獲得的固定利息收入。 |
到期年化收益率 Yield to Maturity,YTM | 債券的到期年化收益率(Yield to Maturity,YTM)是指如果持有該債券直至到期,並且在此期間收到了所有的利息和本金支付,那麼投資者將在債券投資上獲得的年化收益率。YTM考慮了投資者購買債券時的價格、債券的票麵價值(即債券的麵值,到期時投資者將獲得的本金)、債券的到期期限、以及債券上的利息支付頻率等因素(未考慮交易傭金成本)。 按到期收益率對債券所有未來的現金流進行折現,所得到的現值應和買入價格相等,即未來得到的利息支付和最終本金償還的現值總和,應等於債券當前的市場價格。 對於不同的債券品種,YTM的計算公式有所不同:
【以上公式的相關參數】
|
派息頻率 | 派息頻率是指這張國債一般會按照怎樣的時間頻率進行派息,美國國債notes和bonds目前基本都是一年約定兩次派息。 |
剩餘年限 | 剩餘期限是從現在買入至該國債到期,還剩餘多少年限。 |
到期日 | 是指國債的到期日期。 |
交易執行日 Execution date | 交易達成的日期,但還未發生債券所有權的轉移。 |
交易結算日 Settlement date | 交易最終完成的日期,買方必須向賣方付款,同時賣方將資產交付給買方。為執行日後一天。應計利息的計算以結算日為準。 |
買賣盤口 | 買盤上顯示了投資者願意支付的最高價格和該價格對應的到期年化收益率。賣盤上顯示了投資者願意接受的最低價格和該價格對應的到期年化收益率。 債券買賣盤口報價通常隻能作為參考,而不是確定性的交易價格。 |
買入參考價 Bid Price | 買入參考價(Bid Price),指從平台處買入債券的參考價格,T-Bill的報價通常為利率,即Discount Rate;Bond和Note的報價通常為價格。報價不含交易傭金和應計利息。 |
賣出參考價 Ask Price | 賣出參考價(Ask Price),指把自己持有的債券賣出時,買方支付的參考價格。 |
中間價 | 是指市場上的買入價格和賣出價格之間的中間點。投資者可使用中間價作為參考,因為它通常反映了市場上的供需情況。 |
久期 | 久期(Duration)是一個用於衡量債券價格對利率變化的敏感度指標,它可以幫助你預測債券價格在市場利率上升或下降時的變化方向和幅度。 |
麥考利久期 | 麥考利久期(Macaulay Duration) 是債券的一個關鍵金融指標,它表示投資者持有一份特定債券後,收回其投資的平均期限。麥考利久期是對債券的現金流支付時間進行加權平均的結果,包括了債券的本金和利息支付。該指標的數值代表了債券的平均期限,以年為單位。 麥考利久期的意義在於,它幫助投資者了解債券的平均剩餘期限,以及在此期限內所能獲得的現金流。這個指標也用來衡量債券價格對利率變動的敏感度。當麥考利久期較長時,表示債券的現金流主要集中在較遠的將來,因此債券的價格更容易受到市場利率波動的影響。 麥考利久期的數值越高,說明債券的本金回收期較長,價格波動幅度相對較大;反之,麥考利久期較短的債券,在市場利率變動時,其價格波動較小。 |
修正久期 | 修正久期(Modified Duration)是用來衡量債券價格對利率變動的敏感度的指標。它衡量了債券價格在市場利率變動時的相對變化幅度。修正久期的計算基於麥考利久期(Macaulay Duration) 並乘以債券的收益率(或者利率變動的百分比變化)。它通常用來估計債券價格在利率變動時的變化幅度。 在實際應用中,修正久期可用於估算債券價格的變化。例如,如果一個債券的修正久期為5年,那麼當市場利率上升1%時,該債券的價格大約會下降5%。 |
凸性 | 債券的凸性(Convexity)是指債券價格對於利率變化的曲線度量。 它是一個用來衡量債券價格變動相對於利率變動的二階導數。凸性提供了比修正久期(Modified Duration)更精確的信息,因為它考慮了債券價格與利率的非線性關係。 在金融領域,債券價格與市場利率之間的關係通常是非線性的。當利率上升或下降時,債券價格的變化速度並不是線性的,而是呈現出曲線狀。凸性度量了這種非線性關係。 凸性通常用於修正久期的估計,因為它提供了更準確的價格變動信息。修正久期隻考慮了價格和利率之間的線性關係,而凸性則可以提供關於價格和利率之間曲線關係的更詳細信息。在債券組合管理和風險管理中,了解債券的凸性非常重要,因為它有助於更精確地估計債券組合在不同市場利率下的價格變化。 |
應計利息 | 債券的應計利息(Accrued Interest)指的是在債券的最後一個付息日(或稱到期日)之後,但在債券出售日期之前所累積的未付利息。 當投資者在一個付息周期的中間時間購買債券時,他們必須支付截至購買日期的應計利息給賣方。在債券的下一個付息日期,投資者能收到全額的利息。應計利息通常是基於債券的票麵利率和購買日期之間的實際天數進行計算的。 應計利息不是費用,而是買家支付給賣家的持有期間的利息,雖然債券一般是半年才派息一次,但是買入持有之後每天都會計算應計利息,交易時買家需要支付這部分錢給賣家。應計利息會在派息之後清空並重新計算。 其中,C=票息,s = 當前付息期總天數,r = 當前付息期剩餘天數 舉個例子來說明應計利息:2021/12/18發行的5年期note,票息 = 5,到期日為2026/12/18。當前結算日為2023/10/31,下一付息日期為2023/12/18,上一付息日期為2023/06/18. 故:s = 下一付息日 - 上一付息日 = 2023/12/18 - 2023/06/18 = 183天 r = 下一付息日 - 結算日 = 2023/12/18 - 2023/10/31 = 48天 Accrued Interest = 5/2 * (183 - 48) / 183 = 1.84426 暫時無法在飛書文檔外展示此內容 注:執行日(Execution Date)是交易達成的日期,但還未發生債券所有權的轉移; 結算日(Settlement Date)是交易最終完成的日期,買方必須向賣方付款,同時賣方將資產交付給買方。為執行日後一天。 應計利息的計算以結算日為準。 具體的天數根據當期實際天數計算。Bonds and notes issued by the U.S. Treasury earn interest calculated on an actual/actual basis. 所以,如果你在 10 月 31 日購買了這張國債,你需要支付給賣家大約 1.84 美元的應計利息,以補償他應該獲得的利息。然後,在當年的 12 月 18 日,你將獲得全部利息支付。 (注意:以上案例為方便理解,采用應計利息的通用算法,每個機構對於“計息係數”定義不同,需要以實際計算結果為準) |